배열의 합을 구할 때는 배열의 합을 두번 구해 2개의 결과를 도출하는 것보다 배열의 결과 합을 재사용해서
값을 구하는 것이 더 효율적이다. 알고리즘의 연산 시간은 기본 연산의 실행 횟수로 평가되기 때문이다.
알고리즘에서는 실제로 실행되는 연산의 횟수를 계산하는 것이 아니라 복잡도라는 개념을 이용한다.
[ 복잡도 ]
복잡도에는 연산의 횟수를 의미하는 시간 복잡도와 자원 공간의 양을 의미하는 공간 복잡도가 존재한다.
시간복잡도
시간 복잡도 : Big-O 표기법을 이용해서 최악의 경우를 대비한다. ( 최소한의 성능 보장 )
O(1), 상수시간 : 입력한 데이터의 크기와 관계없이 일정한 시간이 소요되는 알고리즘 ( 첫 요소만 출력 )
ex) 배열에 직접 접근 ( 스택, 큐 )
* Big-O 표기법은 상수항을 무시
O(n), 선형시간 : 입력한 데이터의 크기에 비례해서 처리시간이 늘어나는 알고리즘
ex) 반복문을 사용해서 배열의 모든 요소에 접근할 때 ( 배열의 수 만큼 반복 )
O(n^2), 지수시간 : 입력한 데이터 크기의 제곱에 비례해서 처리시간이 늘어나는 알고리즘
ex) 이중 반복문, 삽입정렬, 버블정렬, 선택정렬
O(2^n) : 입력한 데이터 크기의 지수 제곱에 비례해서 처리시간이 늘어나는 알고리즘 ex) 재귀함수
공간 복잡도
공간 복잡도 : 프로그램을 실행시킨 후 완료하기 까지의 필요한 공간의 크기
고정공간 : 코드가 저장되고, 단순히 변수와 상수가 저장되는 공간
가변공간 : 코드가 실행되는 도중에 동적으로 필요한 공간 ( 알고리즘과 연관 )
[ 2일차 과제 ]

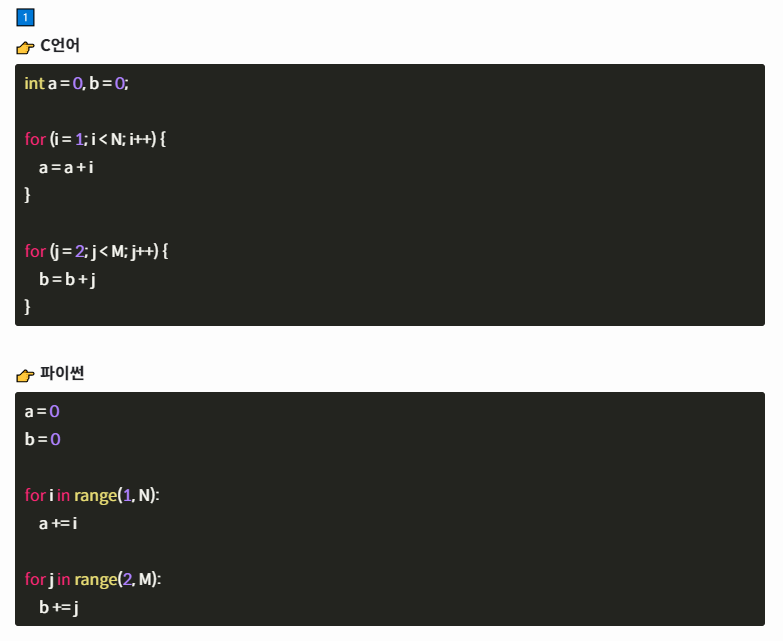
함수 범위 내에 모든 요소에 한번씩 접근하는 반복문을 2번 사용했지만
시간복잡도는 상수항을 무시하기 때문에 시간복잡도는 총 O(n)이다.
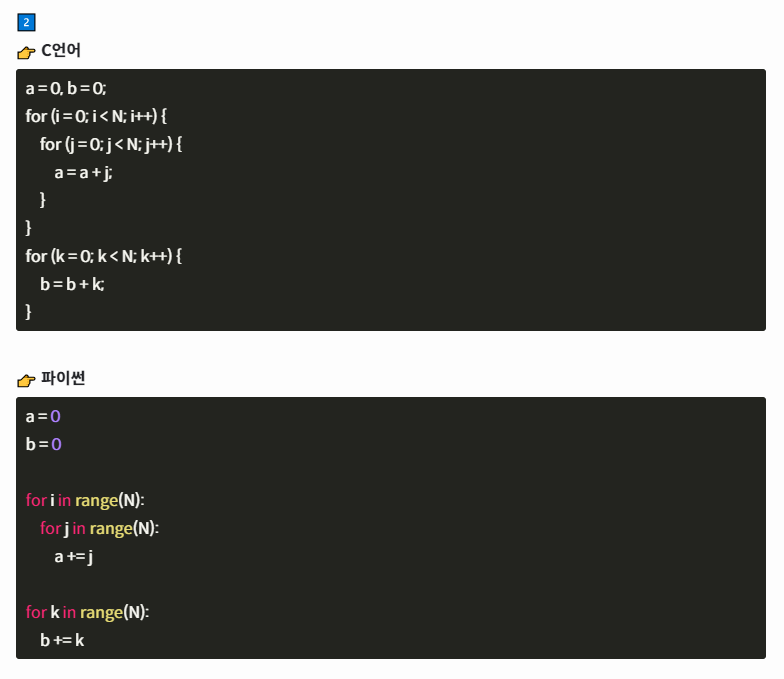
첫번째 반복문은 이중 반복문을 사용해서 요소 접근 횟수가 중첩되기 때문에 O(n^2)이다.
두번째 반복문은 함수 범위 내에 요소에 한번씩 접근하기 때문에 O(n)이다.
최종 시간 복잡도는 O(n^2) + O(n) = O(n^2) 이다.
'Python > [ 모각코 3월 과정 ] 코딩테스트 Level 1' 카테고리의 다른 글
| [ 모각코 코딩테스트 Level 1 3일차 ] 탐색 (0) | 2022.03.10 |
|---|
